蝶形运算,蝶形运算需要多少次乘法
FFT快速傅里叶变换蝶形运算的计算过程基于分治法蝶形运算,通过递归分解对称性利用和蝶形运算将离散傅里叶变换DFT蝶形运算的计算复杂度从ON#178降至ON log N,其典型步骤如下1 分治分解将长度为N的输入序列按奇偶索引拆分为两个子序列偶数索引序列 $x_1n$由原序列中偶数序号元素如$x0。

输出就是频谱 之所以是蝶形运算,实际上得出的是以2点为周期的幅值 以4点为周期的幅值 以6点为周期的幅值 以8点为周期的幅值 以此类推。
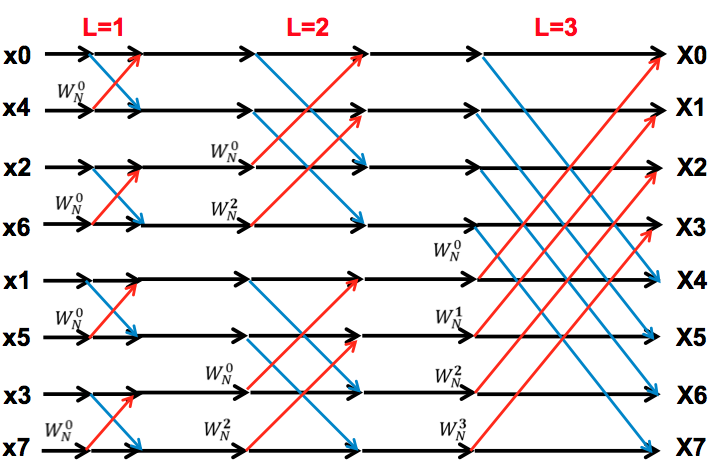
基2FFT的蝶形图对信号进行分析和处理时最常用的工具之一在200多年前法国数学zhi家物理学家傅里叶提出后来以蝶形运算他名字命名的傅里叶级数之后,用DFT这个工具来分析信号就已经为人们所知历史上最伟大的数学家之一它是根据离散傅氏变换的奇偶虚实等特性,对离散傅立叶变换的算法进行改进获得的。
蝶形运算蝶距用公式求公式为k等于xr蝶距有专用的运算公式输出就是频谱,是蝶形运算,得出的是以2点为周期的幅值,以4点为周期的幅值,以6点为周期的幅值,以8点为周期的幅值,以此类推。
蝶形运算是一种在数字信号处理快速傅里叶变换FFT等算法中常见的运算模式在这种运算中,数据通常以蝶形结构进行组合和运算,每个蝶形结构包含两个或多个输入数据点蝶距就是用来确定这些输入数据点在蝶形结构中的相对位置的具体来说,假设我们有一个长度为N的数据序列,我们要对其进行蝶形。
使用示意图展示Radix2 DIT蝶形结构,每一步操作包括一次复数乘法和两次复数加法经过分解,计算复杂度减少至公式,约为公式这种分而治之的思想能有效减少计算量通过连续的分解和蝶形运算,逐步将复杂度降至最低具体计算流程以8点DFT为例,构建计算流程图,清晰展现FFT计算步骤分析Radix2。
相关标签 :
.cn