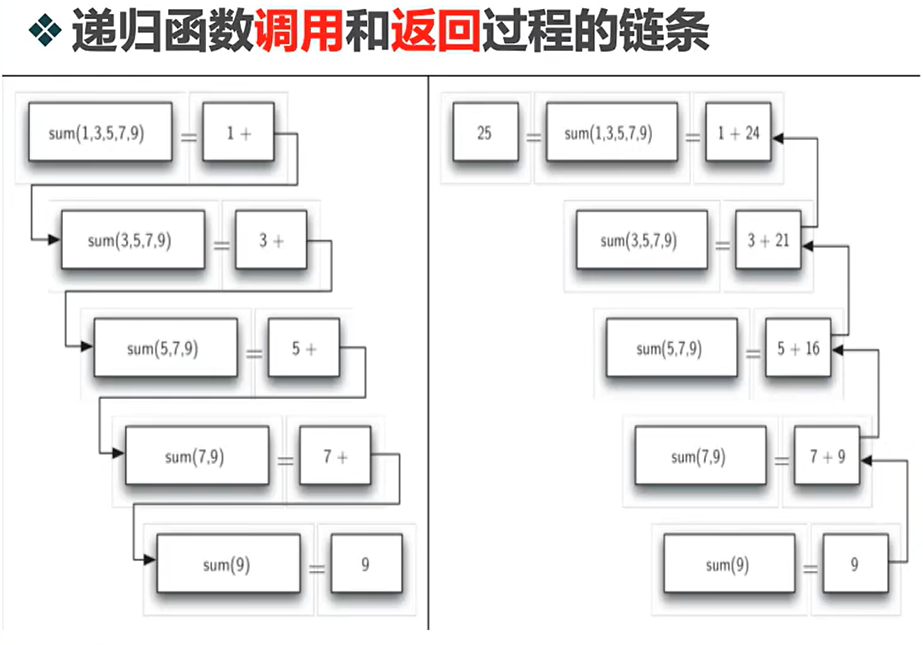
递归算法时间复杂度,递归的时间复杂度如何计算
1、矩阵连乘问题的递归算法时间复杂度为On#179该算法的核心是通过递归函数寻找矩阵链的最优分割点,并计算不同分割方式下的乘法次数,最终确定全局最优解其时间复杂度分析如下1 递归分解与子问题规模递归算法将原问题分解为多个子问题,例如计算矩阵链A#8321A#8322A#8345的最优乘递归算法时间复杂度;最近菜鸡作者苦于解递归方程求解时间复杂度的一些问题 整理一下思路 递归算法的运行时间常用递归表达式表示 本文主要讲解如何从递归表达式求解出时间复杂度 万变不离其宗,总结以下四种形式Tn = Tn1+1 解Tn = Tn1+1 = Tn2+1+1 = Tn2+2 = Tn3+3 = = Tnn+n递归算法时间复杂度;为什么需要Master公式目标快速判定常见递归算法的时间复杂度,避免手工展开递归树的繁琐过程背景许多分治递归算法如快排归并二分搜索树形DP等可表示为统一递推式TN = a · TNb + fN其中a递归分支数子问题数量b子问题规模缩减因子每次递归子问题规模;2 重复计算问题递归将问题分解为多个子问题,若子问题存在重叠部分如斐波那契数列的递归实现,未优化的递归会重复计算同一子问题例如,计算fib5时,fib3和fib2会被多次计算,导致指数级时间复杂度O2#8319而通过记忆化技术缓存已计算结果或迭代方法,可将时间复杂度降至;当n较大时,计算速度会极慢,不适合实际应用迭代和动态规划解法通过循环从数列起始逐步计算后续项,只需遍历一次,时间复杂度为On避免递归算法时间复杂度了递归调用的大量重复计算,性能优于递归解法矩阵快速幂解法利用矩阵运算性质,将时间复杂度优化到Olog n通过快速幂算法减少计算次数,在处理大规模数据;汉诺塔问题的时间复杂度为O2^n时间复杂度的计算用递归来解决汉诺塔问题是非常方便的选择设盘子个数为n时,需要Tn步,把A柱子n1个盘子移到B柱子,需要Tn1步,A柱子最后一个盘子移到C柱子一步,B柱子上n1个盘子移到C柱子上Tn1步得递推公式Tn=2Tn1+1所以。
2、答案D 本题需要用到特定形式的递归式分析法在本题中,a=8,b=2,故符合1的情况时间复杂度为On3a=16,b=4;时间复杂度onlogn的算法是采用“分治思想”,将要排序的数组从中间分成前后两个部分,然后对前后两个部分分别进行排序,再将排序好的两部分合并在一起,这样数组就有序每次划分区域都选择中间点进行划分,所以递归公式可以写成Tn = Tn2 + Tn2 + n, T1 = C常数;理论计算机研究中,衡量算法一般从两个方面分析时间复杂度和空间复杂度空间复杂度跟时间复杂度是类似的,下面简单解释一下时间复杂度对于一个数据规模为n的问题,解决该问题的算法所用时间可以用含有n的函数Tn来表示对于绝大多数情况,只需要了解算法的一般性能而不考虑细节,也就是说,我们只;总的来说是O2^n级别 当然真正实现这个算法的时候不会这么采用暴力的计算如果加入记忆化,把每个Ti的值先记下,则时间复杂度可以降到On^2级别 进一步优化,可以尝试计算这个递归数列的通项不过我简单试了下发现最后要计算1n的和,这个据我所知只能直接计算这样整个算法的复杂度可以降到On至于楼下说的O1的常数做法,我个人没有想到,也许在数据规模小的情况。

3、d 注意到这个函数做的事跟#c的函数恰好相反,算法复杂度相同,也是Ologne 因为已算出#g每次做3n3次加法,那么i从1到n,一共做23*n^25n+6次加法,所以复杂度为On^2f 这个函数可以写成公式Tn=Tn2+Tn1,这个递归式跟黄金分割有关系,解这个递归式;空间复杂度分析主要考虑递归深度最好情况每次都是二分,递归深度为 $Olog n$最坏情况每次划分出一个数值,递归深度为 $On$2 归并排序Merge Sort时间复杂度分析归并排序每次都是二分,时间复杂度为 $Tn = 2Tn2 + On = Onlog n$空间复杂度分析;1,on,on2求解过程为先给出问题规模n的函数的表达式,然后给出其时间复杂度tn但是在现实程序设计过程中,往往遇到的问题都是比较复杂的算法,就不能很容易地写出规模n的表达式,也比较难总结其时间复杂度递归函数就是属于这种情况下面举例说明递归函数的时间复杂度的分析方法。
4、即先进后出,举例说明Maxa,n1调用以后产生的又一个调用函数为Maxa,n2,然后为Maxa,n3一直到n==1的时候结束递归,在计算时,最后一个产生的调用函数先计算,即Maxa,1然后以此往前计算在这个过程中,调用函数调用了n次,时间复杂度为On;主定理Master Theorem是算法分析中用于解决分治和递归算法时间复杂度的有力工具它适用于形如 $Tn = aTleftfracnbright + fn$ 的递归式,其中 $a geq 1$ 是递归调用的数量,$b 1$ 是每次递归将问题规模缩小的因子,$fn$ 是所有递归调用以外的额外工作量主定理的;log n局限性高级主定理不适用于非多项式 fn 或非单调递归式如 Tn=sin n此时需采用递归树法或代入法分析总结高级主定理通过参数化递归关系,高效求解分治算法的渐近复杂度,尤其适用于子问题规模均匀缩减的场景理解其三种情况及参数意义,可快速推导多数递归算法的时间复杂度。