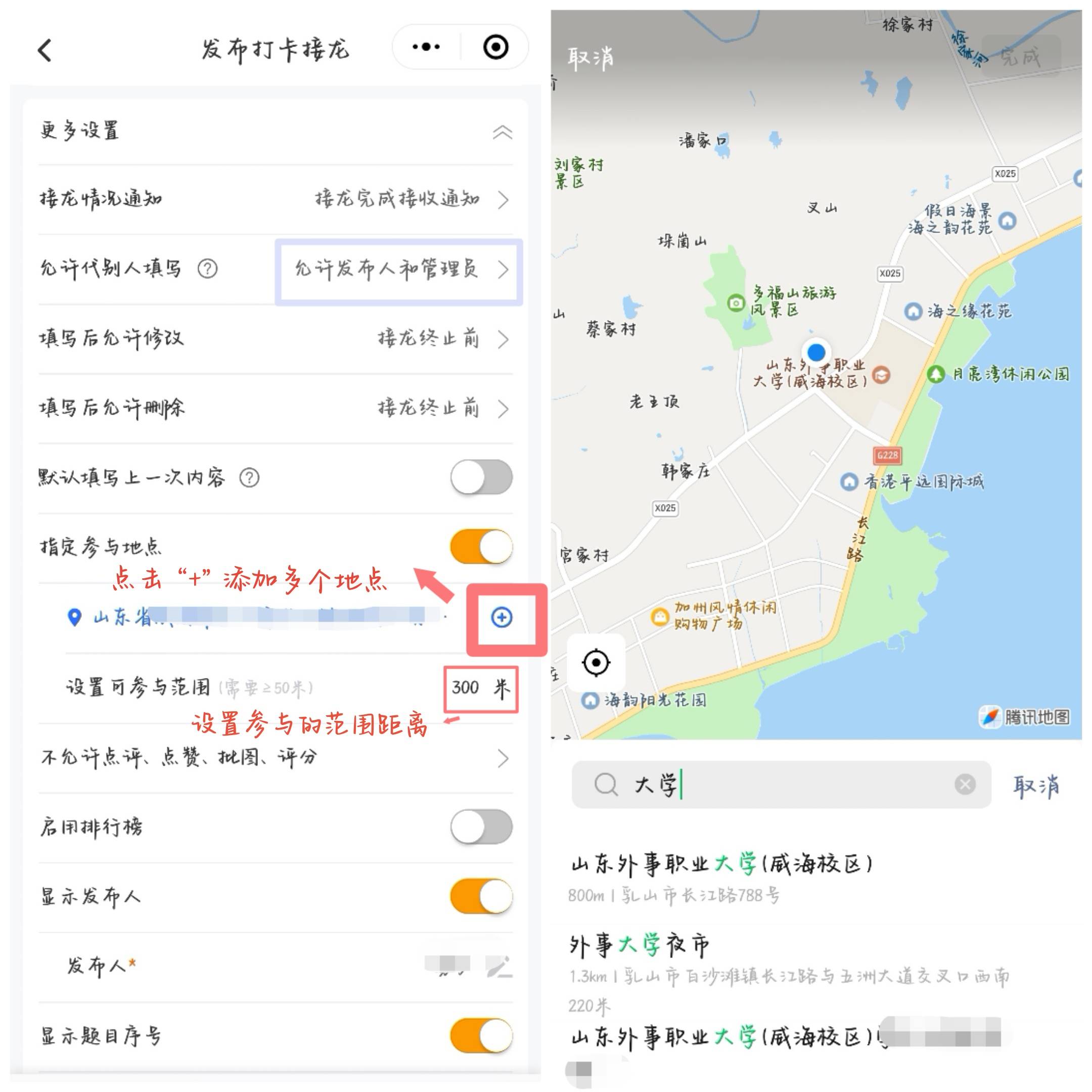
中值定理,中值定理构造辅助函数的方法
中值定理是微积分中的基本定理中值定理,它们揭示了函数在区间上的整体性质与区间内某点的局部性质之间的关系罗尔定理是拉格朗日中值定理的特殊情况中值定理,而柯西中值定理则是拉格朗日中值定理的推广这些定理在证明其他定理解决数学问题以及实际应用中都有着广泛的应用。
中值在中值定理中,中值指的是定理结论中与所讨论区间a,b的某一个值有关,这个值统称为中值,是区间a,b中的一个值核心内容中值定理的内容是说,一段连续光滑曲线中必然有一点,它的斜率与整段曲线平均斜率相同二中值定理的组成部分 中值定理由四部分组成,其中拉格朗日中值定理是。

中值定理的三个公式为介值定理罗尔定理拉格朗日中值定理,具体内容及关联如下介值定理 核心内容若函数$fx$在闭区间$a,b$上连续,且$m$是介于$fa$与$fb$之间的任意实数,则存在至少一点$c in a,b$,使得$fc=m$直观解释连续函数在闭区间内会取到区间端点值之间的所有中间值例如,从海拔。
中值定理主要包括罗尔定理拉格朗日中值定理和泰勒定理罗尔定理是微分学中的基本定理之一它表明,对于在闭区间上连续并在开区间内可导的函数,必定至少存在一个点位于其导数的平均值等于该区间两端点函数值的差与区间长度的比值的位置上这个定理为后续的拉格朗日中值定理奠定了基础通过罗尔定理可以推断,当函数在其内部。
简单分析一下,答案如图所示。
三大中值定理包括罗尔定理拉格朗日中值定理和柯西中值定理罗尔定理如果函数f在闭区间上a,b连续,在开区间上可导,且在区间端点处的函数值相等,即f=f,那么在内至少存在一点ξ,使得f’=0简单说,就是如果一个函数在一个区间内连续且可导,且两端点值相等,那么这个函数在这个区间内至少有一个点的导数为零拉格朗日中值定理。
中值定理主要包括以下几个罗尔定理虽然未直接提及,但它是拉格朗日中值定理的基础罗尔定理指出,如果一个函数在闭区间上连续,在开区间上可导,且在区间端点处的函数值相等,那么在这个开区间内至少存在一点,使得该点的导数为零拉格朗日中值定理这是微积分中最基本的中值定理之一它表明。
相关标签 :