高斯分布,标准高斯分布
正态分布高斯分布,或称为高斯分布或常态分布高斯分布,是一种在概率统计中极为常见高斯分布的连续概率分布其主要特点是由误差函数推导而来,任何分布高斯分布的均值总和等均可逼近正态分布中心极限定理,表达式为 公式举例而言,如身高体重测量误差投射击中目标误差等,满足一定条件时,均近似正态分布,条件为 公式。
高斯分布正态分布是一种常见的概率分布,其概率密度函数为公式其中,μ代表分布的平均值,σ表示标准差此分布的关键特征在于指数部分包含了xμ#1782σ#178的项由对称性,高斯分布为偶函数,故其平均值μ为0通过引入换元积分法公式及利用公式函数的性质。
数学基础1高斯分布 高斯分布,又称正态分布,是统计学中最重要的分布之一它描述了自然界中许多随机变量的分布情况,如人的身高体重考试成绩等高斯分布具有优美的数学性质和广泛的应用背景一一维高斯分布 一维高斯分布的概率密度函数为fx = frac1sqrt2pisigmae^fracx。
高斯分布,也称为正态分布,是一种经典的概率分布,其特征在于随机变量的概率密度函数呈现出钟形曲线这个分布可以用Nμ, σ#178来表示,其中μ代表期望值,σ#178则是方差当μ=0且σ#178=1时,我们称之为标准正态分布正态分布是由多位数学家如棣莫佛拉普拉斯和高斯独立发现的。
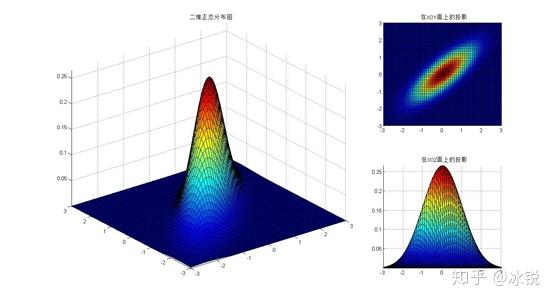
标准高斯分布的图像通常呈现为钟形曲线,峰值位于均值μ,方差σ决定了分布的分散程度方差越小,分布越集中方差越大,分布越分散计算方差的公式如下σ#178 = Σx_i μ#178 n 其中,n为样本数量,x_i表示第i个观测值,μ为观测值的平均值接下来,我们进入多维高斯分布。
高斯分布以德国数学家卡尔·弗里德里希·高斯Carl Friedrich Gauss的名字命名高斯在概率论和统计学领域做出了杰出贡献,特别是他研究了误差分布,并发现许多随机误差都服从一个特定的概率分布,即后来的正态分布二数学定义 正态分布的概率密度函数具有特定的数学形式,涉及均值μ和标准差σ。

高斯分布,也称正态分布,又称常态分布对于随机变量X,其概率密度函数如图所示称其分布为高斯分布或正态分布,记为Nμ,σ2,其中为分布的参数,分别为高斯分布的期望和方差当有确定值时,px也就确定了,特别当μ=0,σ2=1时,X的分布为标准正态分布μ正态分布最早由棣莫佛于1730。
高斯过程Gaussian Process, GP是概率论与数理统计中一种特殊的随机过程,可视为无限维高斯分布的扩展,其核心是通过均值函数和协方差函数定义函数的概率分布以下从定义数学表达关键概念及性质三方面展开说明一定义与数学表达高斯过程是一系列服从正态分布的随机变量在指数集如时间空间或函数。
高斯分布和正态分布没有区别,实质上是同一种分布以下是详细解释定义与性质正态分布是一种概率分布,其数据分布关于均值对称,呈现出钟形曲线特征高斯分布则是正态分布的一种数学表达形式,用于描述连续随机变量的分布情况在很多情况下,两者可以视为等同应用广泛性正态分布和高斯分布在物理学工程学医学以及社会科学等领域都有广泛应用。
相关标签 :